1984/04 Wandtapijt

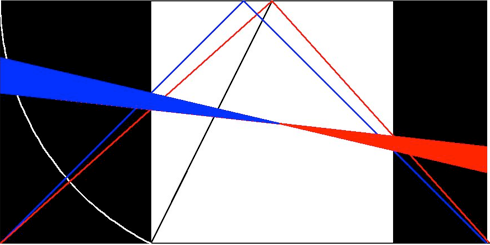
In Le Corbusier’s 'universal instrument to face the ever present problem of proportioning', developed between 1942 and 1948, he tried to reconcile several systems of measuring and proportioning as they were used in nature, art, architecture and industry. Systems like the decimalized metric system of measurements versus the imperial system of units that still refers back to the mathematics of the human body, or proportioning systems like the irrational golden ratio versus the rational Fibonacci sequence and graphical systems to create harmonious compositions, like regulating lines and the 'place of the right angle', all these combined with systems of normalization and standardization used by the industry. In 1943 Le Corbusier turned his 'dream of a universal grid of proportions' into a design task for his young collaborator Hanning with the following instructions:

"Take a man-with-arm-upraised, 2.20 m. in height; put him inside two squares, 1.10 by 1.10 meters each, superimposed on each other; put a third square astride these first two squares. This third square should give you a solution. The 'place of the right angle' should help you to decide where to put this third square.

With this grid for use on the building site, designed to fit the man placed within it, I am sure you will obtain a series of measures reconciling human stature (man-with-arm-upraised) and mathematics".

However even with the help of Elisa Maillard (an expert on regulating lines) a perfect reconciliation of the double square with the golden section and the 'place of the right angle' is mathematically impossible.

This raises the (also ever present) question of absolute perfection agains practicality in design. How Le Corbusier dealt with this question can be illustrated by the way he married his initial metric 'Modulor-man' based on a man of 1.75 (man-with-arm-upraised is 2.16 = 2 x 1.08 m.) with the imperial system of feet, using the argument 'that in English detective novels, the good-looking men, such as the policemen, are always six feet tall'. That's why the final 'Modulor-man' became 'exactly' six feet, which is (182.88 cm) practically 1.83 m. (man-with-arm-upraised is 2.26 = 2 x 1.13 m.). From this 'good-looking six foot man' he then developed two golden-ratio series of measurements, a red series featuring 1.83 and the bleu series featuring 2.26 (the double square of 1.13 m., which together with 0.70 is again the golden means of 1.83).

For me, while thinking about a design for this tapestry, there was an intriguing analogy between Le Corbusier's 'Modulor', or better to say his search for precision on one side and his idea of practicality on the other side. A tapestry, as one should know, starts with a needlepoint canvas, a very fine mesh of little square openings through which afterwards the different threads of the rug will have to be knotted by hand. In fact needlepoint canvas is a very precise grid that in a way digitizes the image you would like to create on top of it. Further, since the needlepoint canvas is a fabric, it is rather flexible, so it is difficult to keep a straight line really straight and next to that the length of the knotted threads will influence the actual image depending on the direction in which they are brushed.

Thus the design for this tapestry in a way paraphrases the 'Modulor' and its abstract reasoning (its metaphysical dimension) by means of an image that changes its 'reality' depending on once line of sight (parallax).

Animation film

How to construct the ‘Modulor’ with a pair of compasses and a ruler

next >

< previous